Machine Learning : Perceptron, Linear Regression
Perceptron#
Intro#
- 深度學習基礎單元(神經元)
- Linear classifier
Perceptron Learning Algorithm#
基本定義#
- 資料 : (x,y)⇒(x1,x2)
- 方程式 : w0c+w1x1+w2x2=(w0,w1,w2)⋅(c,x1,x2)=0
- 資料點位於直線右側時, 等式結果為正, 反之則為負
基本算法 : 修正錯誤#
- 遇到錯誤的點時將往x方向的法向量加入w, 迫使資料點被放置於直線的另一側
 img
img處理高維度資料#
- 訂立一個 threshold, 取內積結果與 threshold 相差的正負值
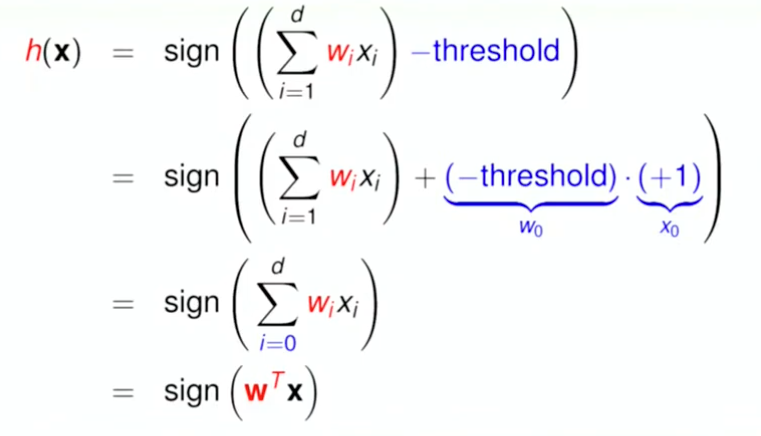 img
img關於迭代次數與參數正確性成正相關的證明#
當 \mathbf w^{(t)}\ 對樣本 (xk,yk) 分類錯誤時,PLA會做以下更新 :
w(t+1)=w(t)+ykxk假設現在是第t次 :
w(t+1)⋅w\*=(w(t)+ykxk)⋅w\*=w(t)⋅w\*+yk(xk⋅w\*)線性可分 ⇒yk(xk⋅w\*)≥γ
w(t+1)⋅w\*≥w(t)⋅w\*+γ接著計算更新之後的Norm :
∥w(t+1)∥2=∥w(t)+ykxk∥2=∥w(t)∥2+2ykw(t)⋅xk+∥xk∥2≤∥w(t)∥2+0+R2(∵ykw(t)⋅xk≤0)=∥w(t)∥2+R2M次更新後可得 :
∥w(M)∥2≤MR2並且可以分別得到dot至少成長 :
w(M)⋅w\*≥Mγ以及norm至多成長 :
∥w(M)∥≤RM因此可以得到Cosine的下界 :
cosθM=∥w(M)∥∥w\*∥w(M)⋅w\*≥(RM)∥w\*∥Mγ=R∥w\*∥Mγ其中右式為單調增加
雜訊容忍#
不過由於需要minimize的為indicator, 無法解開(NP-hard), 可改進此演算法
Pocket Algorithm#
- 更新模式與PLA相同
- 若新的權重優於原版才更新為新的 wt
Linear Regression#
Intro#
- 與Perceptron很類似, 不過不是取sign, 是取內積作為函數的output
- 以擬合資料走向為目標, 想辦法最小化殘差量
Error measure#
使用的誤差平方
 imgs
imgsAlgorithm#
先定義資料集 {(xi,yi)}i=1n,xi∈Rp :
X=11⋮1x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1px2p⋮xnp,β=β0β1⋮βp,y=y1y2⋮yn模型就會是 :
y^=Xβ接著定義Loss:
J(β)=∥y−Xβ∥22=(y−Xβ)⊤(y−Xβ)接著求微分,然後令他為0 (求解正規方程) :
∂β∂J=−2X⊤(y−Xβ)=!0⟹X⊤Xβ=X⊤y假設 X⊤X 可逆(大部分情況都是可逆) :
β=(X⊤X)−1X⊤yApplications#
線性回歸也可套用到二元分類, 利用公式去推算初始的線, 加快算法的收斂速度
 img12
img12 




