Intro#
- 把許多神經元合成一個layer
- 藉由多個layer去把input映射到output
- 對整個模型的權重 Wij 去做學習
- 為深度學習之基礎
Activation function#
- 用來決定一個節點是否要激活
- 同時用於normalize節點輸出
- 共分為以下三類
- Binary step
- Linear step : 無法用於預測不同input對應的weight
- Non-Linear step : 允許堆疊layer, backpropagation
常見的非線性激活函數 : Sigmoid, tanh, ReLU, Leaky ReLU
Sigmoid#
- 輸出介於0與1
- 用於概率輸出
- 由於輸出中心非0, 會造成梯度下降時方向偏移, 而影響收斂速度
Tanh#
- 輸出介於-1與1 (以0作為中心)
- 相較Sigmoid有更大動態範圍
- 輸入過大時, 也容易發生梯度消失
ReLU#
f(x)=max(0,x)
- 可緩解梯度消失
- 在負區為零可提升特徵表示之泛化能力
- 不過若輸入包含大量負數, 會導致死亡ReLU
Leaky ReLU#
- 與ReLU非常雷同, 不過在負區時加入一個斜率
- 額外的參數可能影響performance
Architecture of Deep Learning#
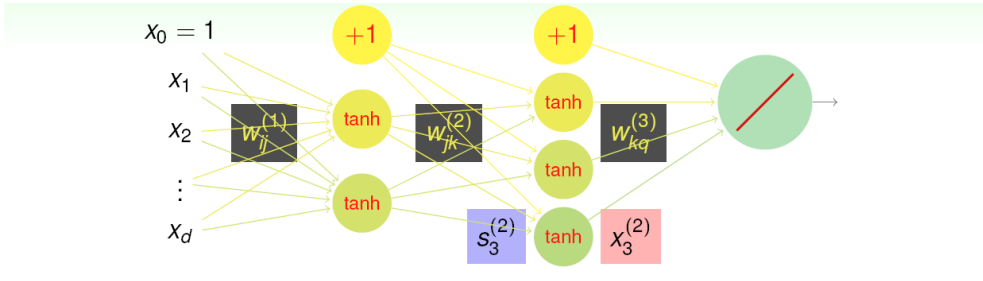 img13
img13在每層layer要對下一層進行輸出時, 會在權重上再額外加上一個常數維度, 舉例:
在 3-5-1 的NNet中, 共有如下數目的weight:
(3+1)×5+(5+1)×1=26
Error measure#
使用誤差平方:
en=(yn−NNet(xn))2=(yn−i=0∑dL−1wi1(L)xiL−1)2接著計算誤差的偏微分, 可以幫助隨機梯度下降的進行
Partial derivatives on layers#
∂sj(L)∂en=−2(yn−sj(L))∂wij(L)∂(∑iwij(L)xi(L−1))=xi(L−1)Chain rule:
∂wij(L)∂en=∂sj(L)∂en⋅∂(∑iwij(L)xi(L−1))∂sj(L)⋅∂wij(L)∂(∑iwij(L)xi(L−1))=−2(yn−sj(L))xi(L−1)考慮當前layer的輸出:
sj(l)=f(i∑wij(l)xi(l−1))可以再分解成後面的誤差+激活函數的微分
∂wij(l)∂en==∂sj(l)∂en⋅f′(i∑wij(l)xi(l−1))⋅xi(l−1)
Compute delta#
這邊假設激活函數用的是tanh
δj(l)=∂sj(l)∂en=k∑(δk(l+1)∂xj(l)∂sk(l+1))⋅∂sj(l)∂xj(l)
Backpropagation Algorithm#
- 初始化權重(隨便設定)
- 先隨便挑一筆資料用來更新weight, SGD / Mini-batch
- 做forward pass, 取得網路對於 xn 的輸出:
xj(l)=tanh(sj(l))=tanh(i∑wji(l)xi(l))
- 對於每層中的每個神經元計算誤差信號, 其中delta會用到後面層數的輸出(根據上面chain rule推導)
- 更新權重:
wij(l)←wij(l)−ηδj(l)xi(l)其中eta用以控制更新幅度, 透過梯度下降去讓誤差函數收斂
Gradient Descent#
前面的偏微分求出的結果就是梯度, 並且可以發現往梯度的反方向移動就可以讓loss function收斂:
wt+1=wt−η∇Ein(wt)其中的v為梯度向量的反方向:
v=−∥∇Ein(wt)∥∇Ein(wt)
Neural Network Optimization#
- Non-convex : 很難找到對於global的最佳解
- Local minimum : 由於backprop, 通常來說不同的初始權重會導致不同的收斂結果
- 通常需要嘗試多種不同的初始權重
- Difficult, but practically works
Shallow vs Deep NNet#
- 淺層的網路更容易訓練
- 淺層網路架構更簡單
- 但深度網路可以完成更複雜的任務, 例如電腦視覺


