Intro#

• 具有記憶的神經網路
• 適合處理序列資料 (NLP)

在每一步RNN都會通過當前的輸入與隱藏狀態計算出現在的隱藏狀態 :

然後再把隱藏狀態轉換成輸出 :

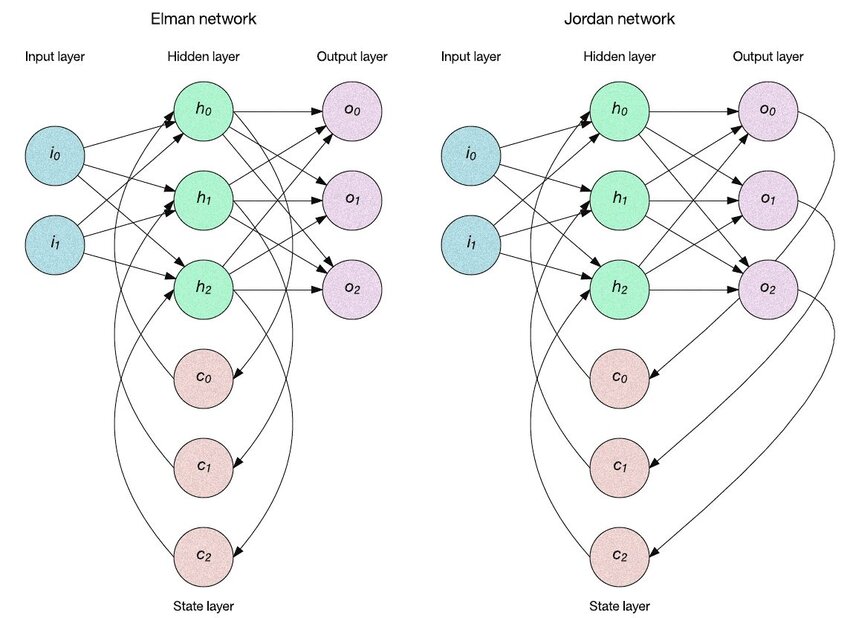
Jordan Network#

Elman Network的recurrent經過延遲後作為現在這個layer的輸入，但Jordan是把輸出層當作記憶

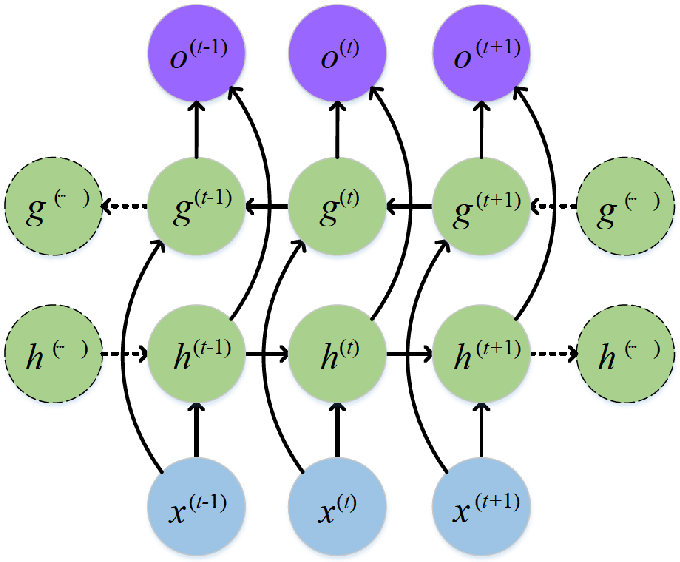
Bidirectional Network#

當序列資料整筆都是可預測的 (例如NLP任務)，利用雙向RNN可以更好的理解上下文

RNN的缺點#

• 遺忘資訊 : 因為每個時間步模型都會更新隱藏狀態 (矩陣乘法)，如果權重小於1，就會導致前一個隱藏狀態的影響快速縮小
• 訓練不穩定
  • 使用時間反向傳播 (BPTT)，在每個時間點上展開成一個前向傳播的NN
  • 反向傳播一直乘權重 + 激活，導致梯度消失
  • 反之則會導致梯度指數增長，需要引入正則化

RNN的優點#

• 高靈活性 : 可以處裡多種序列對序列的架構 (一對一、一對多、…)
• 用途 : 圖像描述(一對多) / 語意分類(多對一) / 翻譯(多對多) / 影片分類(多對多) / 文本生成(一對多/多對多)

LSTM#

• 用來解決長距離依賴
• 顯式記憶 (記憶細胞)
• 加上Gate來控制記憶單元的進出流量 (正則化)

Memory Cell#

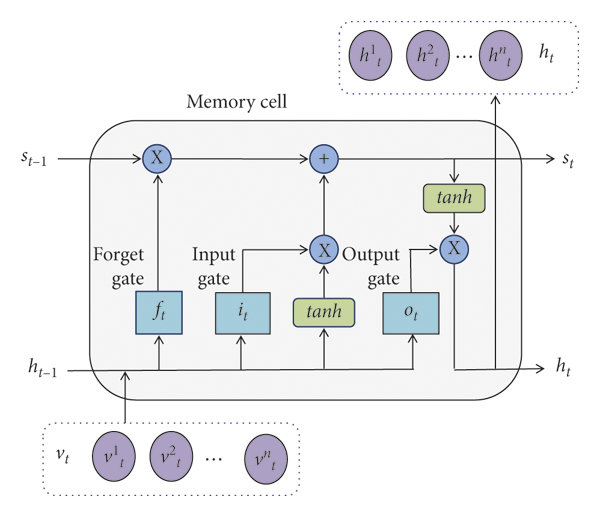
圖中沒有標明的矩陣操作都是加法

• 輸入 :

  • 當前的輸入
  • 前一個隱藏狀態
  • 前一個記憶

• 輸出 :

  • 更新後的隱藏狀態、記憶
  • 輸入、輸出閘門，遺忘閘門 (使用Sigmoid, 0-1可以用來表示開關程度)
  • 候選記憶 (tanh)

• 記憶細胞 ($\mathbf{C}_t$) 是一個向量

  • 資訊在裡面流動，保持不變
  • 遺忘閘門 : 用來決定是否遺棄舊的記憶
  • 輸入閘門 : 控制輸入

• 輸出閘門先用Sigmoid生成，接著與縮放過後的記憶(tanh)做乘法，得到 $\mathbf{h}_t$

可以總結如下 :

• $f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)$
• $i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)$
• $o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)$
• $C_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)$ (候選記憶)
• $C_t = f_t * C_{t-1} + i_t * \tilde{C}_t$ (用舊的記憶 + 現在的候選記憶)
• $h_t = o_t * \tanh(C_t)$

BPTT#

• 在時間點上展開、梯度下降 : $w \leftarrow w - \eta \frac{\partial L}{\partial w}$
• 學習權重以及bias權重 : $W_i, W_o, W_f, b_i, b_o, b_f, W_C, b_C$

GRU#

• 更新閘門同時控制前一個隱藏狀態以及新增輸入的保留量 : $z_t = \sigma(W_z \cdot [h_{t-1}, x_t])$
• 重製閘門用來控制計算候選記憶時的重製量 : $r_t = \sigma(W_r \cdot [h_{t-1}, x_t])$
• 候選記憶 : 先重製再與輸入做加法 : $h_t = \tanh(W \cdot [r_t * h_{t-1}, x_t])$
• 最後用加權平均生成記憶 : $h_t = (1 - z_t) * h_{t-1} + z_t * \tilde{h}_t$
• 參數更少，更好訓練

Forecasting#

• 需注意資料量、資料品質、趨勢、意外事件…
• RNN以外的方法 : 自回歸、移動平均模型
• RNN的優勢 : 抗躁能力強、同時支援線性/非線性、多變數、多步預測
• LSTM with Attention : 權衡不同時間的重要性，專注在比較重要的那幾筆資料
  • 用來預測故障 (智慧製造)

Reference#

• Jordan Network
• Bidirectional RNN
• Long-Short Term Memory