Intro
$$ G(x) = \sum_{c=1}^{C} [b(x) = c] G_c(x) $$
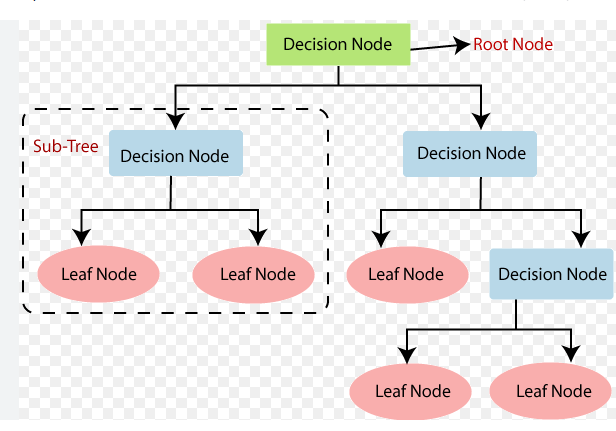
Basic Decision Tree Algorithm
當還未滿足終止條件時，執行 :
- 學一個分割準則 $b(x)$
- 當前節點分割 : $\mathcal{D}$ to $C$ parts $\mathcal{D}_c = {(x_n, y_n): b(x_n) = c}$
- 分割出來的子集再做遞迴呼叫 : $G_c \leftarrow DecisionTree(\mathcal{D}_c)$
- 返回當前節點的預測函數 : $G(x) = \sum_{c=1}^{C} [b(x) = c] G_c(x)$
C&RT (Classification and Regression Tree) Algorithm
Branching
- 選擇最佳分割準則
- 總是創造二元樹
- 基於leaf的最佳常數 : $g_t(x) = E_{y|\text{optimal constant}}$
Purifying
- 用一個簡單的閾值做二元分類
- 純化節點 : $b(x) = \underset{\text{decision stumps } h(x)}{\operatorname{argmin}} [D_c \text{ with } h] \cdot \text{impurity}(D_c \text{ with } h)$
Some Metrics
- Regression Error : $\text{impurity}(\mathcal{D}) = \frac{1}{N} \sum_{n=1}^{N} (y_n - \bar{y})^2$
- Classification Error : $1 - \max_{1 \le k \le K} \frac{\sum_{n=1}^{N} \mathbb{I}(y_n = k)}{N}$
- Gini Index : $1 - \sum_{k=1}^{K} \left( \frac{\sum_{n=1}^{N} \mathbb{I}(y_n = k)}{N} \right)^2$
Algorithm
- 邊界條件 : 不能再做分支
- 學一個分割準則 : $b(x) = \underset{\text{decision stumps } h(x)}{\operatorname{argmin}} [D_c \text{ with } h] \cdot \text{impurity}(D_c \text{ with } h)$
- 考慮最佳的樹樁 : $\mathcal{D}_c = {(\mathbf{x}_n, y_n) : b(\mathbf{x}_n) = c}$ ，切出兩個子集
- 遞迴
- 返回組合之後的模型 : $G(\mathbf{x}) = \sum_{c=1}^{2} \mathbb{I}(b(\mathbf{x}) = c) G_c(\mathbf{x})$
Regularize
- Pruning
- 做決策樹時，同時把複雜度加入懲罰項
- 先長出完全樹，再去每一步選擇能最小化 (Error + 複雜度) 的node
Branching on Categorial Features
- 可以根據出現率 / label相關性排序，再做類似數值特徵的閾值分類
Surrogate Branch
- 關鍵的特徵剛好缺值
- 在訓練時對每個 $b(x)$ 就先算一次次要分裂，想辦法用其他特徵構造出效果差不多的樹樁
- 遺失資料時可以用替代路徑做分類
Properties
決策樹優勢
- 易於理解和視覺化
- 能處理數值和類別特徵
- 自動特徵選擇
複雜資料集處理
- 多維特徵空間分割
- 複雜決策邊界學習
Adaptive Boosting
- 結合弱分類器最後集成一個強大的分類器
Boostrap (Re-Weighting)
- 對原始資料做抽樣(有重複，不平均)
- 每個Learner想辦法最小化誤差
如果每次只是隨機Boostrap，Base Learner會太相似，重採樣強迫學習不同的解
Optimal Re-Weighting
- 假設當前Base Learner的錯誤率是 : $\epsilon_t = \frac{\sum_{n} u_n^{(t)} \mathbb{I}[y_n \neq g_t(x_n)]}{\sum_{n} u_n^{(t)}}$
- 我們希望更新權重之後對錯各半，因此 :
- 錯分的資料乘 $(1 - \epsilon_t)$
- 分好的資料乘 $\epsilon_t$
- Normalization
- Scaling Factor : $\phi_t = \sqrt{\frac{1 - \epsilon_t}{\epsilon_t}}$
依照Scaling Factor的定義，假如當前Base Learner的效果很好，則會把錯分的資料加權到超大，把注意力轉移到更難分類的樣本
AdaBoost Algorithm
- 先初始化權重(一開始大家都一樣) : $u_n^{(1)} = 1/N$
- 進行迭代 :
- 訓練弱分類器 $g_t$ ，最小化 $\epsilon_t = \frac{\sum_{n=1}^{N} u_n^{(t)} \mathbb{I}[y_n \neq g_t(x_n)]}{\sum_{n=1}^{N} u_n^{(t)}}$
- 計算 $\phi_t = \sqrt{(1 - \epsilon_t) / \epsilon_t}$，更新權重 $u^{(t)} \rightarrow u^{(t+1)}$ :
- 分類錯誤的權重乘以 $\phi_t$
- 分類正確的權重除以 $\phi_t$
- 令 $\alpha_t = \ln \phi_t$ (越準確的 $g_t$，$\alpha_t$ 越大)，越大代表在最終決策有更大權重
- 最後輸出分類器 : $$G(x) = \text{sign}\left(\sum_{t=1}^{T} \alpha_t g_t(x)\right)$$
Decision Stump as Base Learner
- 做一個簡單的樹樁來二元分類 : $h(x) = s \cdot \text{sign}(x_i - \theta)$
- 目標是找最佳的分裂方向，可以先對特徵值進行排序
- 暴力搜索參數($(\theta, i, s)$)，總複雜度是 $O(d \cdot N \log N)$